दो या दो से अधिक संख्याओं का लघुत्तम समापवर्त्य वह छोटी से छोटी संख्या हैं जो उन संख्याओं से पूरी तरह विभाजित हो जाती हैं।
जैसे:- 4, 8, 12 का लघुत्तम समापवर्त्य = 2 × 2 × 2 × 3 = 24
अतः अभीष्ट लघुत्तम समापवर्त्य 24 वह छोटी से छोटी संख्या हैं जो 4, 8, 12 तीनों से पूरी-पूरी तरह विभाजित हो जाती हैं।
अपवर्त्य या गुणज (Multiple): लघुत्तम समापवर्त्य निकालने का तरीका
अपवर्त्य या गुणज (Multiple)
अपवर्त्य या गुणज (Multiple) :- किसी संख्या का अपवर्त्य वे सभी संख्याएँ होती हैं जिसमें उस संख्या से पूर्ण भाग किया जाता हैं।
3 और 6 संख्या 18 के गुणनखंड है । यहाँ 18, संख्या 3 और 6 का गुणज अथवा अपवर्त्य (Multiple) है। इसी प्रकार 48 = 4 x 12 यह दर्शाता है कि 4 और 12, संख्या 48 के अपवर्तक हैं तथा 48, 4 और 12 का एक अपवर्त्य है। अपवर्त्य को गुणज भी कहते हैं।
किसी संख्या में प्राकृतिक संख्याओं (1, 2, 3, …… ) से गुणा करने पर उस संख्या के विभिन्न गुणज अथवा अपवर्त्य प्राप्त होते हैं।
- 2 के गुणज अथवा अपवर्त्य-2, 4, 6, ……
- 3 का अपवर्त्य = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
- 4 का अपवर्त्य = 4, 8, 12, 16, 20, 24, 27, 32, 36, 40
- 5 के गुणज अथवा अपवर्त्य-5,10, 15, ……
- 16 के अपवर्त्य- 16,32,48, 64, …… आदि।
समापवर्त्य (Common Multiple) की अवधारणा
| संख्या | अपवर्त्य |
| 3 6 9 | 3,6,9,12,15,18 …… 6,12,18, …… 9,18,27, …… |
तीनों संख्याओं में संख्या 18 समान अपवर्त्य है। अतः उपरोक्त संख्या का समापवर्त्य 18 है। संख्याओं के समान अपवर्त्यों को उनका समापवर्त्य कहते हैं।
उपरोक्त सारणी से,
- कोई संख्या अपने प्रत्येक अपवर्तक का अपवर्त्य होती है।
- किसी संख्या का प्रत्येक अपवर्त्य उस संख्या से बड़ा या उसके बराबर होता है।
- प्रत्येक संख्या स्वयं का एक अपवर्त्य है।
- किसी संख्या के अपवर्त्यों की संख्या असीमित होती है।
यह भी जाने-
किसी भी संख्या में से उसके अंकों का योगफल घटाने पर प्राप्त अन्तर सदैव 9 का अपवर्त्य होता है।
उदाहरणार्थ कोई एक संख्या 4253 लेते हैं। अब देखते है कि इस संख्या के अंकों का योगफल
=4+2+5+3=14
अब संख्या 4253 में से अंकों का योगफल 14 घटाने पर प्राप्त अन्तर
=4253-14
=4239
=9×471
अतः अंतर 9 का अपवर्त्य है।
जब आप 8 में 5 का गुणा करते हैं तो गुणनफल 40 प्राप्त होता है।
यहाँ 8 x 5 = 40 में, 8 गुण्य, 5 गुणक तथा 40 गुणनफल है। 8 व 5 को 40 का गुणनखंड कहते हैं।
लघुत्तम समापवर्त्य निकालने का तरीका
- अभाज्य गुणनखण्ड विधि द्वारा
- भाग विधि द्वारा
(a). अभाज्य गुणनखण्ड विधि द्वारा
सर्वप्रथम दी गई संख्या को अभाज्य गुणनखण्डों के रूप में व्यक्त करें। फिर इन संख्याओं के सभी अभाज्य गुणनखण्डों के सबसे बड़े घातांकों वाली संख्याओं का प्राप्त गुणनखण्ड ही लघुत्तम समापवर्त्य हैं।
उदाहरण 1. 32, 64 तथा 128 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
हल:- प्रश्नानुसार,
32 ⇒ 2 × 2 × 2 × 2 × 2 = 2⁵
64 ⇒ 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
48 ⇒ 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
लघुत्तम समापवर्त्य = 2, 3 की सबसे बड़े घातांकों वाली संख्याओं का गुणनफल = 2⁶ × 3¹
लघुत्तम समापवर्त्य = 96
उदाहरण 2. 12, 48, 72 तथा 120 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
हल:- प्रश्नानुसार,
12 = 2 × 2 × 3 = 2² × 3¹
48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3¹
72 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3¹ × 5¹
लघुत्तम समापवर्त्य = 2, 3 तथा 5 की सबसे बड़ी घातों वाली संख्याओं का गुणनफल = 2⁴ × 3² × 5¹
लघुत्तम समापवर्त्य = 16 × 9 × 5
लघुत्तम समापवर्त्य = 720
Ans. 720
(b). भाग विधि द्वारा
उदाहरण 3. 24, 48, 96, 192 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
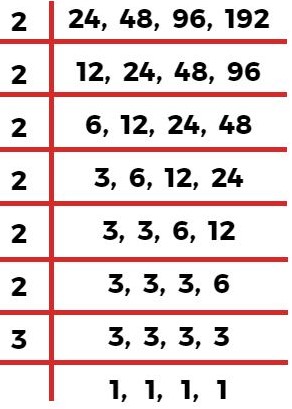
लघुत्तम समापवर्त्य = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁶ × 3¹
लघुत्तम समापवर्त्य = 192
उदाहरण 4. 32, 56, 78, 120 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
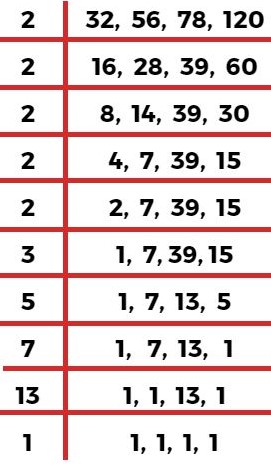
लघुत्तम समापवर्त्य = 2 × 2 × 2 × 2 × 2 × 3 × 5 × 7 × 13
लघुत्तम समापवर्त्य = 32 × 15 × 91
लघुत्तम समापवर्त्य = 43,680
भिन्नों का लघुत्तम समापवर्त्य
भिन्नों का लघुत्तम समापवर्तक (L.C.M.) = अंशों का लघुत्तम समापवर्त्य / हरों का महत्तम समापवर्तक
उदाहरण 5. 7/9, 14/15 तथा 7/10 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
हल:- प्रश्ननानुसार,
दी गई भिन्नों का लघुत्तम समापवर्त्य = 7, 14, 7 का लघुत्तम समापवर्त्य / 9, 15, 10 का महत्तम समापवर्तक
= 14/1
= 14
उदाहरण 6. 2/5, 3/4, 1/9 तथा 7/10 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
हल:- प्रश्ननानुसार,
दी गई भिन्नों का लघुत्तम समापवर्त्य = 2, 3, 1, 7 का लघुत्तम समापवर्त्य / 5, 4, 9, 10 का महत्तम समापवर्तक
= 42/1
= 42
घातांक का लघुत्तम समापवर्त्य
(a). जब दी गयी संख्याओं का आधार समान हो, तो सर्वाधिक घात वाली संख्या ही दिए गए संख्याओं का लघुत्तम समापवर्त्य होगा।
उदाहरण 7. 5¹, 5², 5⁴, 5⁶ तथा 5¹² का ल स ज्ञात कीजिए?
हल:- समान आधार पर 5 हैं। तथा अधिकतम घात 5¹² का हैं।
लघुत्तम समापवर्त्य = 5¹²
उदाहरण 8. 5⁻¹, 5⁻², 5⁻⁴, 5⁻⁶ तथा 5⁻¹² का ल. स. ज्ञात कीजिए?
हल:- आधार 5 समान हैं तथा अधिकतम घात 5⁻¹ की हैं।
लघुत्तम समापवर्त्य = 5⁻¹
(b). जब आधार समान नहीं हो तथा आधार में कोई उभयनिष्ठ गुणन खण्ड नहीं हो, तो दिए गए संख्याओं का गुणनखण्ड ही लघुत्तम समापवर्त्य होगा।
उदाहरण 9. 5³ तथा 2³ का लघुत्तम समापवर्त्य = 5³ × 2³
लघुत्तम समापवर्त्य = 5 × 5 × 5 × 2 × 2 × 2
लघुत्तम समापवर्त्य = 125 × 8
लघुत्तम समापवर्त्य = 1000
दशमलव संख्याओं का लघुत्तम समापवर्त्य
(a). सबसे पहले दशमलव के बाद अधिकतम अंकों वाली संख्या का पता लगाइए।
(b). यदि दशमलव के बाद अधिकतम दो अंक हो, तो सभी अंकों में 100 से गुणा करके उसे पूर्ण संख्या में बदल देगें।
अगर दशमलव के बाद अधिकतम तीन, चार या पाँच अंक हो, तो उसमें क्रमशः 1000, 10000 या 100000 से गुणा करके उसे पूर्ण संख्या में बदल देगें।
(c). प्राप्त पूर्ण संख्याओं का लघुत्तम समापवर्त्य ज्ञात करेंगें। उसके बाद प्राप्त लघुत्तम समापवर्त्य में 100, 1000, 10000 से गुणा किया गया था। भाग देने के बाद जो संख्या प्राप्त होगी वही दी गई संख्याओं का लघुत्तम समापवर्त्य होगा।
उदाहरण 10. 0.12, 4.8, 0.72 तथा 1.20 का लघुत्तम समापवर्त्य ज्ञात कीजिए?
हल:- यहाँ दशमलव के बाद अधिकतम दो अंक हैं। इसलिए सभी संख्याओं को 100 से गुणा करने पर प्राप्त संख्या = 12, 480, 72, 120
इन संख्याओं का लघुत्तम समापवर्त्य = 1440
अभीष्ट लघुत्तम समापवर्त्य = 1440/100
लघुत्तम समापवर्त्य = 14.40