[MSNC11] पूर्ण संख्या , प्राकृत संख्याएँ पूर्णांक संख्या और संख्या रेखा

प्राकृत संख्याएँ (Natural Number)

गणना करते समय 10 संकेतों 1,2,3,4,5,6,7,8,9,0 का उपयोग किया जाता है तथा गणना का कार्य 1 से प्रारंभ होता है। इन्हीं अंकों को मिलाकर प्राकृत संख्याएँ लिखी जाती हैं। गणना के लिए जिन संख्याओं का उपयोग किया जाता है उन्हें प्राकृत संख्या(Natural Number) कहते हैं।
प्राकृत संख्याओं के समूह को N से दर्शाते हैं।
अर्थात् प्राकृत संख्या (N) = 1,2,3, …. आदि।

सबसे छोटी प्राकृत संख्या 1 है।

प्राकृतिक संख्याओं का फार्मूला

• प्रथम n प्राकृतिक संख्याओं का औसत = (n+1) /2
• लगातार n तक विषम प्राकृतिक संख्या का योग = (n/2+1)
• प्रथम n प्राकृतिक सम संख्याओं का औसत = n+1
• प्रथम n प्राकृतिक विषम संख्याओं का औसत = n
• लगातार n तक विषम प्राकृतिक संख्याओं का औसत = (n+1) /2

प्राकृत संख्याओं के गुण (Properties of Natural numbers)

• दो प्राकृत संख्याओं का आपस में योग करने से या गुणा करने पर प्राकृत संख्या ही प्राप्त होती है।
• दो प्राकृत संख्याओं का आपस में व्यवकलन (घटाना) या भाग करने से सदैव प्राकृत संख्या प्राप्त नही होती है।
• दो प्राकृत संख्याओं को किसी भी क्रम में जोड़ सकते हैं। दो प्राकृत संख्याओं को किसी भी क्रम में गुणा कर सकते हैं। अर्थात प्राकृत संख्याओं के लिए क्रमविनिमय का नियम योग व गुणन संक्रिया में लागू होता है जबकि घटाने एवं भाग संक्रिया पर लागू नही होता।
• प्राकृत संख्याओं के लिए साहचार्य नियम योग एवं गुणा संक्रिया में लागू होता है जबकि घटाने एवं भाग संक्रिया में लागू नहीं होता।
• प्राकृत संख्याओं के लिए गुणा का योग व अन्तर पर बंटन (वितरण) होता है।
• किसी प्राकृत संख्या मे एक से गुणा या भाग करने पर संख्या का मान नही बदलता।
• इस प्रकार a,b,c तीन प्राकृत संख्याओं के लिए
  • (a+b) एक प्राकृत संख्या है।
  • (axb) एक प्राकृत संख्या है।
  • a-b सदैव एक प्राकृत संख्या हो आवश्यक नही है।
  • a+b सदैव एक प्राकृत संख्या हो, जरूरी नही है।

Questions

41600 तथा 41006 में कौन सी संख्या बड़ी है?

1 से 100 के बीच की संख्याएँ लिखने के लिए कितने बार 9 का प्रयोग करना पड़ता है?

चार अंकों की सबसे बड़ी प्राकृत संख्या तथा तीन अंकों की सबसे छोटी प्राकृत संख्या के बीच का अंतर निकालिए ?

पूर्ण संख्या : पूर्ण संख्याओं पर संक्रियाएँ (Whole Number)

प्राकृतिक संख्याओं (1, 2, 3, 4, ……) में शून्य (0) को सम्मिलित करने पर जो संख्याएँ प्राप्त होती हैं, पूर्ण संख्याएँ कहलाती हैं। पूर्ण संख्याओं को W से प्रदर्शित करते हैं। या फिर इसे इस तरह से भी परिभाषित किया जा सकता हैं “शून्य ‘0’ से लेकर अनंत तक की संख्याओं को पूर्ण संख्याएँ कहते हैं।” उदाहरण: 0, 1, 2, 3, 4, ……। ∞ आदि

स्मरणीय बिंदु:

• शून्य (0) सबसे छोटी एवं पहली पूर्ण संख्या है।
• सभी प्राकृतिक संख्याएँ पूर्ण-संख्याएँ हैं।
• चूंकि प्रत्येक पूर्ण संख्या से बड़ी पूर्ण संख्याएँ होती हैं अतः कोई भी पूर्ण संख्या सबसे बड़ी पूर्ण संख्या नहीं होती है।

पूर्ण संख्याओं के गुण

• प्राकृत संख्या के सभी गुण पूर्ण संख्याओं के लिए भी सही हैं।
• सबसे छोटी पूर्ण संख्या 0 है।
• संख्या रेखा पर 0 से दाहिने ओर क्रमशः पूर्ण संख्या बढ़ते क्रम में दिखायी गयी है। अर्थात् 0+1 = 1,1+1 =2, … , 101 + 1 = 102, 102 + 1 = 103, 103 + 1 = 104, … , इत्यादि।
• संख्या रेखा पर दाहिने ओर से बाँए ओर का क्रम घटते क्रम में है, जैसे ….. 4,3,2,1,0
• सबसे बड़ी पूर्ण संख्या नहीं दिखाई जा सकती। क्योंकि यदि आप कोई बड़ी से बड़ी संख्या सोचते हैं तो उसमें एक जोड़ कर उसकी अगली बड़ी संख्या प्राप्त की जा सकती है। जो उस संख्या की परवर्ती संख्या होगी।

योग का संवरक गुण: 

जब किसी दो पूर्ण संख्याओं का आपस में जोड़ा जाता हैं तो प्राप्त योगफल सदैव पूर्ण संख्या होता है, यह पूर्ण संख्याओं के योग का संवरक प्रगुण है।

उदाहरणार्थ:-11 + 9 = 20 इन दोनों संख्याओं का योग 20 एक पूर्ण संख्या है।

योग का क्रम-विनिमेय गुण: 

जब किसी दो पूर्ण संख्याओं को जोड़ा जाता हैं तो उनके योगफल पर संख्याओं के क्रम का कोई प्रभाव नहीं पड़ता है, इसे ही योग का क्रम-विनिमेय प्रगुण है।

उदाहरणार्थ: 14 + 33 = 47
33 + 14 = 4

योग का तत्समक अवयव: 

किसी पूर्ण संख्या में यदि शून्य को जोड़ा जाता है तो योगफल वही संख्या प्राप्त होती है। इसी कारण शून्य को पूर्ण संख्याओं में योग का तत्समक अवयव कहते हैं।

शून्य को पूर्ण संख्याओं के लिए योज्य तत्समक भी कहते हैं।
उदाहरणार्थ: 3 + 0 = 0 + 3 = 3

योग का साहचर्य गुण: 

तीन पूर्ण संख्याओं को क्रम में जोड़ते समय किन्हीं दो पूर्ण संख्याओं का समूह पहले बना लेने से योगफल में अंतर नहीं पड़ता है, यह योग संक्रिया का साहचर्य प्रगुण है।

उदाहरणार्थ: (11+33) +102 = 11+ (33+102) = 11+33+102

पूर्ण संख्याएँ एवं पूर्ण संख्याओं पर संक्रियाएँ

रहीम के पास 100 पेज की एक कॉपी है जिसमें उसने 80 पेज पर गणित तथा 20 पेज पर विज्ञान का कार्य किया है। उसकी इस कॉपी में कितने पेज शेष बचे?

50 की पूर्ववर्ती संख्या 49 है 17 की पूर्ववर्ती संख्या 16 है। क्या शून्य की भी पूर्ववर्ती संख्या होगी?

रामू की माँ ने रामू को 5 लड्डू दिए। रामू ने 2 लड्डू मोहन को खिला दिये और 3 रामू ने खा लिये। अब रामू के पास कितने लड्डू बचे?

यहाँ प्राकृत संख्याओं (Natural Numbers) और पूर्ण संख्याओं (Whole Numbers) से संबंधित कुछ MCQs दिए गए हैं:

MCQ:

निम्नलिखित में से कौन-सी प्राकृत संख्याओं का सेट है?

• a) {0, 1, 2, 3, 4, 5}
• b) {1, 2, 3, 4, 5}
• c) {−1, 0, 1, 2, 3}
• d) {0, −1, −2, −3, −4}

उत्तर: b) {1, 2, 3, 4, 5}

निम्नलिखित में से पूर्ण संख्याओं का समूह कौन-सा है?

• a) {0, 1, 2, 3, 4}
• b) {1, 2, 3, 4, 5}
• c) {−1, −2, 1, 2, 3}
• d) {−1, 0, 1, 2, 3}

उत्तर: a) {0, 1, 2, 3, 4}

प्राकृत संख्याओं का सबसे छोटा मान कौन-सा है?

• a) 0
• b) 1
• c) −1
• d) 2

उत्तर: b) 1

पूर्ण संख्याओं का सबसे छोटा मान कौन-सा है?

• a) 0
• b) 1
• c) −1
• d) 2

उत्तर: a) 0

निम्नलिखित में से कौन-सा कथन सही है?

• a) सभी प्राकृत संख्याएँ पूर्ण संख्याएँ होती हैं।
• b) सभी पूर्ण संख्याएँ प्राकृत संख्याएँ होती हैं।
• c) 0 एक प्राकृत संख्या है।
• d) −1 एक पूर्ण संख्या है।

उत्तर: a) सभी प्राकृत संख्याएँ पूर्ण संख्याएँ होती हैं।

कौन-सा विकल्प केवल पूर्ण संख्याएँ दर्शाता है?

• a) {1, 2, 3, 4, 5}
• b) {0, 1, 2, 3, 4}
• c) {−1, 0, 1, 2, 3}
• d) {1, −2, 3, −4, 5}

उत्तर: b) {0, 1, 2, 3, 4}

निम्नलिखित में से कौन-सा संख्या समूह प्राकृत संख्याओं का नहीं है?

• a) {1, 2, 3, 4, 5}
• b) {0, 1, 2, 3, 4}
• c) {2, 3, 4, 5, 6}
• d) {1, 3, 5, 7}

उत्तर: b) {0, 1, 2, 3, 4}

निम्नलिखित में से कौन-सा कथन सही है?

• a) 0 प्राकृत संख्या है।
• b) 0 पूर्ण संख्या है।
• c) −1 पूर्ण संख्या है।
• d) 0 और −1 दोनों प्राकृत संख्याएँ हैं।

उत्तर: b) 0 पूर्ण संख्या है।

संख्या 1 किसके अंतर्गत आती है?

• a) केवल प्राकृत संख्याएँ
• b) केवल पूर्ण संख्याएँ
• c) प्राकृत और पूर्ण दोनों संख्याएँ
• d) इनमें से कोई नहीं

उत्तर: c) प्राकृत और पूर्ण दोनों संख्याएँ

पूर्णांक संख्या और संख्या रेखा /Integers and Number Lines

पूर्णांक संख्या के प्रकार

पूर्णांक संख्याएँ तीन प्रकार की होती हैं।

1. धनात्मक पूर्णांक

एक से लेकर अनंत तक की सभी धनात्मक संख्याएँ धनात्मक पूर्णांक कहलाती हैं।

कोई भी पूर्णांक संख्या जिसके आगे धनात्मक या ऋणात्मक का कोई चिन्ह नहीं लगा हो ऐसी संख्याएँ पूर्णांक संख्याएँ कहलाती हैं।

उदाहरण :- 1, 2, 3, 4, 5, 6, 7, 8, 9, …………. ∞

ये सभी संख्याएँ धनात्मक पूर्णांक के अंतर्गत आती हैं।

धनात्मक संख्याएँ पूर्णांक संख्या रेखा पर शून्य के दायीं और स्थित होती हैं अतः ये संख्याएँ धनात्मक पूर्णांक के अंतर्गत आएगी।

2. ऋणात्मक पूर्णांक

1 से लेकर अनंत तक कि सभी ऋणात्मक संख्याएँ ऋणात्मक पूर्णांक कहलाती हैं।

• ऋणात्मक पूर्णांक संख्यायों के आगे ऋणात्मक चिन्ह लगा होता है।
• ऋणात्मक संख्याएँ संख्या रेखा पर शून्य के बायीं और स्थित होती हैं।
• जो संख्याएँ शून्य से छोटी होती है वे ऋणात्मक पूर्णांक कहलाती हैं।

उदाहरण :- -1, -2, -3, -4, -5, -6, -7, -8, -9 ……..……∞

ये सभी संख्याएँ ऋणात्मक पूर्णांक के अंतर्गत आती हैं।

3. उदासीन पूर्णांक

ऐसा पूर्णांक जो न तो कोई धनात्मक पूर्णांक है और न ही ऋणात्मक पूर्णांक है। उदासीन पूर्णांक कहलाता हैं यह शून्य पूर्णांकों के अंतर्गत आता हैं।

उदाहरण :-  0

पूर्णांक संख्या के महत्वपूर्ण तथ्य

• संख्या 0, 1, -1, 2, -2, 3, -3, ……….…….∞ पूर्णांक संख्या कहलाती हैं।
• संख्या +1, +2, +3, +4, ……………∞ धनात्मक पूर्णांक कहलाती हैं।
• संख्या -1, -2, – 3, – 4, ……………….∞ पूर्णांक कहलाती हैं।
• संख्या 0, + 1, + 2, + 3, + 4, ऋणेत्तर पूर्णांक कहलाते हैं।
• सभी धनात्मक पूर्णांक संख्या रेखा पर 0 के दायीं ओर तथा सभी ऋणात्मक पूर्णांक संख्या रेखा पर 0 के बायीं ओर स्थित होते हैं।
• ऋणेत्तर पूर्णांक पूर्ण संख्या ही कहलाती हैं।
• दो पूर्णांक जिनका योग शून्य हो एक-दूसरे के योज्य प्रतिलोम कहलाते हैं। ये एक दूसरे के ऋणात्मक भी कहलाते हैं।

पूर्णांकों का जोड़ना, घटाना, गुणा एवं भाग

दो पूर्णांकों के योग का नियम

• (-) + (-) = (+)
• (+) + (+) = (+)
• (-) + (+) = (-)
• (+) + (-) = (-)

समान चिन्ह वाले पूर्णांक का जोड़ :-

विभिन्न चिन्ह वाले पूर्णांकों का जोड़ :-

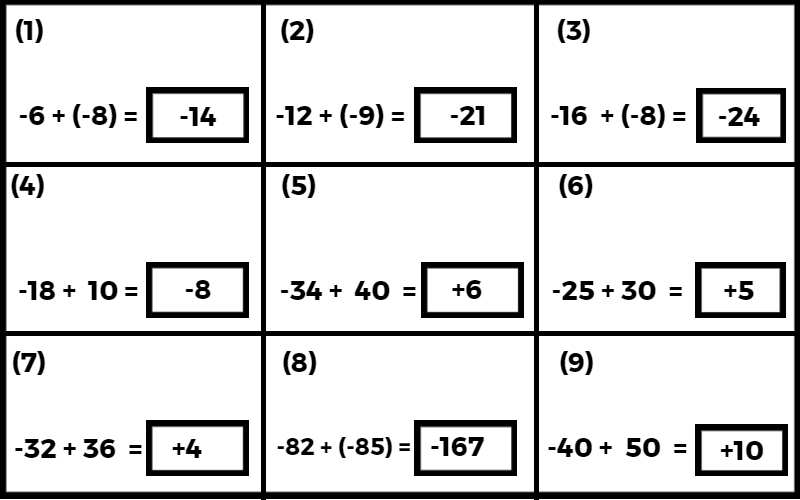
दो पूर्णांकों को घटाने के नियम

• (-) – (-) = (-)
• (+) – (+) = (-)
• (-) – (+) = (+)
• (+) – (-) = (+)

समान चिन्ह वाले पूर्णांकों को घटाना :-

विभिन्न चिन्ह वाले पूर्णांकों को घटाना :-

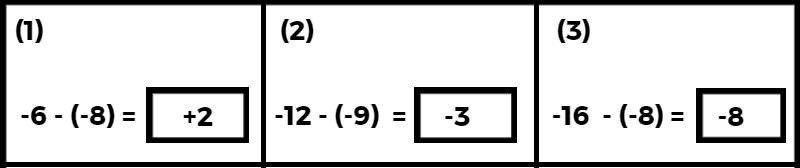
दो पूर्णांकों के गुणनफल का नियम

• (-) × (-) = (+)
• (+) × (+) = (+)
• (-) × (+) = (-)
• (+) × (-) = (-)

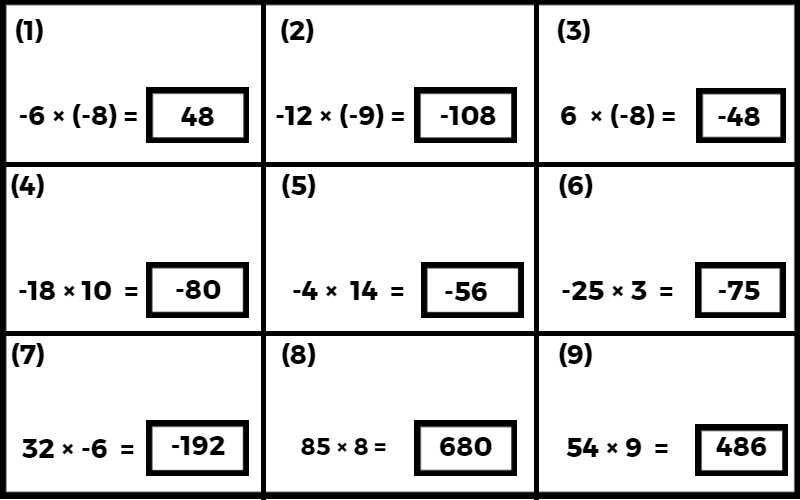
दो पूर्णांकों के विभाजन के नियम

• (-) ÷ (-) = (+)
• (+) ÷ (+) = (+)
• (-) ÷ (+) = (-)
• (+) ÷ (-) = (-)

शून्य के दाँईं ओर प्राकृत संख्याएँ हैं और बाँयी ओर ऋणात्मक संख्याएँ। धनात्मक संख्याएँ, ऋणात्मक संख्याएँ तथा शून्य को मिलाकर पूर्णांक बनते हैं। (I) = { … …………..- 3,-2,1,0,1,2,3,4,5 ………… } आदि।

जिस प्रकार सबसे बड़ी पूर्ण संख्या नहीं है उसी प्रकार सबसे बड़ी पूर्णांक भी नहीं है। क्या आप सबसे छोटी पूर्णांक सोच सकते हैं ?

• धनात्मक पूर्णांकों का योगफल सदैव धनात्मक पूर्णांक तथा दो ऋणात्मक पूर्णांकों का योगफल सदैव ऋणात्मक पूर्णांक होता है।
• एक धनात्मक एवं एक ऋणात्मक पूर्णांक का योगफल धनात्मक पूर्णांक होगा यदि धनात्मक पूर्णांक का आंकिक मान अधिक हो तथा योगफल ऋणात्मक होगा यदि ऋणात्मक पूर्णांक का आंकिक मान अधिक हो।
• पूर्णांकों को जोड़ने में उन सभी गुणों का पालन होता है। जिनका पूर्ण संख्याएँ पालन करती है। दो पूर्णांकों का योग एक पूर्णांक ही होगा।
• सभी पूर्णांकों के योग में क्रम विनिमय नियम लागू होता है।
• दो पूर्णांकों का योग हमेशा एक पूर्णांक संख्या होती है, यही पूर्णांकों के योग के लिए संवरक नियम है।
• पूर्णांकों में शून्य जोड़ने पर उनके मान में कोई परिवर्तन नहीं आता है।

योज्य प्रतिलोम / योज्य तत्समक

5 में क्या जोड़े कि शून्य प्राप्त हो?
अर्थात् 5+ (-5) = 0 (योज्य तत्समक)
इसी प्रकार (-7) में क्या जोड़े कि शून्य प्राप्त हो?
अर्थात् (-7) + (+7) =0 (योज्य तत्समक)
यहाँ (-5) योज्य प्रतिलोम है 5 का तथा + 7 योज्य प्रतिलोम है (-7) का।
अतः किसी संख्या का योज्य प्रतिलोम वह संख्या है जिसे उस संख्या के साथ जोड़ने पर योज्य तत्समक (शून्य) प्राप्त होता है।
संख्या + संख्या का योज्य प्रतिलोम = योज्य तत्समक

पूर्णांक संख्या से संबंधित प्रश्न उत्तर

Q.1 पूर्णांकों के युग्मों के योग ज्ञात कीजिए?

(1). -6, – 2
(a). 10
(b). -10
(c). 4
(d). -4

हल:- -6 और – 4 दोनों के चिन्ह ऋण हैं।
अतः -6 + (-4) = -(6 + 4)
Ans. -10

(2). +8, – 2
(a). 10
(b). -10
(c). 6
(d). -6

हल:- +8 और -2 के चिन्ह विपरीत हैं।
अतः +8 + (-2) = 8 – 2
Ans. 6

Q.2 घटाइए?

(1). -5 में से 3
(a). 2
(b). -2
(c). 8
(d). -8

हल:- 3 का योज्य प्रतिलोम = – 3 हैं।
अतः -5 – 3 = -5 + (-3)
= – (5 + 3)
= – 8

(2). -8 में से -2
(a). 6
(b). -6
(c). 10
(d). -10

हल:- -2 का योज्य प्रतिलोम = 2 हैं।
अतः -8 – (-2) = -8 + (+2)
= – 8 + 2
= – 6

Q.3 -9 और -2 के बीच में कितने पूर्णांक हैं?

(a). 6
(b). 8
(c). 4
(d). 10

हल:- -9 और – 2 के बीच पूर्णांक -8, -7, -6, -5, -4, और -3 हैं।
अतः -9 और -2 के बीच 6 पूर्णांक हैं।

Q.4 परिकलित कीजिए?

1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
(a). -2
(b). -3
(c). -5
(d). 5

हल:- 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10
= (1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8 + 1 + 0)
= 25 – 30
= – 5

Q.5 दो पूर्णांकों का योग 56 हैं। यदि इनमें से एक पूर्णांक – 32 हैं। तो दूसरा पूर्णांक ज्ञात कीजिए?

(a). 55
(b). 66
(c). 77
(d). 88

हल:- प्रश्नानुसार,
दोनों पूर्णांकों का योग 56 हैं। इसलिए दूसरा पूर्णांक 56 में से (-32) घटाने पर प्राप्त होगा।
= 56 – (-32)
= 56 + 32
= 88

Q.6 अंक 0, 1, 2, 3, 4, 5, 6, 7, 8 और 9 को इसी क्रम में लिखिए तथा इनके बीच में ‘+’ या ‘-‘ इस तरह रखिए कि 5 प्राप्त हों?

(a). 3
(b). 5
(c). 7
(d). 9

हल:- 0 + 1- 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9
= (0 + 1 + 3 + 5 + 7 + 9) – (2 + 4 + 6 + 8)
= 25 – 20
= 5