किसी समतल पर कोई वस्तु जितना स्थान घेरती है वह उसका क्षेत्रफल होता है।
क्षेत्रफल का मात्रक वर्ग इकाई होता है।
क्षेत्रफल : त्रिभुज और चतुर्भुज का क्षेत्रफल
त्रिभुज का क्षेत्रफल

आयत का क्षेत्रफल = लम्बाई ग चौड़ाई
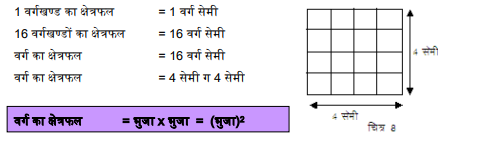
वर्ग का क्षेत्रफल = भुजा x भुजा = (भुजा)2
एक आयत की लम्बाई 7 सेमी व चौड़ाई 3 सेमी है, इसका क्षेत्रफल ज्ञात कीजिए।
समान्तर चतुर्भुज का आधार =क्षेत्रफल/ऊँचाई
समान्तर चतुर्भुज का ऊँचाई =क्षेत्रफल/आधार
समान्तर चतुर्भुज का क्षेत्रफल = आधार x ऊँचाई
उस समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए, जिसका आधार 26.5 सेमी तथा शीर्ष लंब 7 सेमी है।
उस समान्तर चतुर्भुज का आधार ज्ञात कीजिए, जिसका क्षेत्रफल 390 वर्ग सेमी तथा शीर्ष लंब 26 सेमी हो।
उस समान्तर चतुर्भुज का शीर्ष लंब ज्ञात कीजिए, जिसका क्षेत्रफल 1200 वर्ग मीटर और आधार 60 मीटर है।
चतुर्भुज का क्षेत्रफल

समलंब चतुर्भुज का क्षेत्रफल (Area of a Trapezium)
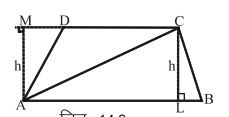
एक ऐसा चतुर्भुज जिसकी दो सम्मुख भुजाएँ एक-दूसरे के समान्तर होती हैं। ABCD एक समलंब चतुर्भुज दिखाया गया है। भुजा AB भुजा DC के समान्तर है। दो समान्तर भुजाओं की लम्बवत दूरी को AM तथा CL से दर्शाया गया है।
यदि हम इस त्रिभुज का विकर्ण AC खींचे इससे समलंब चतुर्भुज दो त्रिभुज ABC तथा ACD प्राप्त होते हैं।
अतः समलंब चतुर्भुज ABCD का क्षेत्रफल = त्रिभुज ABC का क्षेत्रफल + त्रिभुज ACD का क्षेत्रफल
समलंब चतुर्भुज ABCD का क्षेत्रफल = 1/2 AB XCL+ 1/2 DCXAM
चूंकि CL तथा AM समलंब चतुर्भुज की ऊंचाई है अतः यह बराबर होगी। माना कि यह h के बराबर है।
समलंब चतुर्भुज का क्षेत्रफल = 1/2 AB x h + 1/2 DC x h
यदि AB =b1 एवं DC=b2 है तो
समलंब चतुर्भुज का क्षेत्रफल = 1/2 b1 xh+1/2 b2x h
= 1/2(b1+b2)xh
= 1/2 X (समांतर भुजाओं का योग) उनके बीच की दूरी
समलंब चतुर्भुज का क्षेत्रफल = 1/2 X (समांतर भुजाओं का योग) ऊँचाई
समलंब चतुर्भुज का क्षेत्रफल = 1/2 x (b1 + b2) x h
अभ्यास
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके विकर्ण 24 सेमी व 10 सेमी हैं।
एक समचतुर्भुज की एक भुजा 7.5 सेमी और शीर्ष लंब 4 सेमी है तो उसका क्षेत्रफल ज्ञात कीजिए।
एक समलंब चतुर्भुज की समांतर भुजाएं 20 मी व 8 मी है। इन भुजाओं के बीच की दूरी 12 सेमी है, इसका क्षेत्रफल ज्ञात कीजिए।
आधार 30 सेमी और 24.4 सेमी वाले समलंब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए यदि शीर्ष लंब 1.5 सेमी है।
एक समलंब चतुर्भुज का क्षेत्रफल 105 वर्ग सेमी तथा ऊंचाई 7 सेमी है, समान्तर भुजाओं में से यदि एक दूसरी से 6 सेमी अधिक है तो दोनों समान्तर भुजाएं ज्ञात करो।
आयताकार पथ का क्षेत्रफल
एक 25 सेमी लंबी तथा 10 सेमी चौड़े चित्र के बाहर चारों ओर 2 सेमी चौड़ाई की पट्टी बनी है। पट्टी का क्षेत्रफल ज्ञात कीजिए।
एक आयताकार खेल का मैदान 35 मी X 25 मी माप का है। इसके बीचों-बीच लम्बाई के समान्तर 3 मीटर चौड़ा तथा चौड़ाई के समान्तर 2 मीटर चौड़ा रास्ता है। रास्ते का क्षेत्रफल ज्ञात कीजिए।
एक बास्केटबॉल का मैदान 28 मीटर लम्बा तथा 15 मीटर चौड़ा है। इसके बाहर चारों ओर 5 मीटर चौड़ी समतल दर्शक दीर्घा बनानी है। दीर्घा का क्षेत्रफल तथा दर्शक दीर्घा को बनाने का खर्च 5.25 रुपये प्रति वर्ग मीटर की दर से ज्ञात कीजिए।
वृताकार मार्ग का क्षेत्रफल
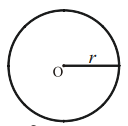
यदि एक वृत जिसकी त्रिज्या r है तो परिधि C= 2nr
तथा क्षेत्रफल = nr2 होता है।
जहां n एक नियतांक है जिसका मान लगभग या 3.14 होता है।
दो सकेन्द्री वृत्तों की त्रिज्याएं क्रमशः 9 सेमी व 12 सेमी हैं दोनों वृत्तों के बीच बनने वाले वृत्ताकार मार्ग का क्षेत्रफल ज्ञात कीजिए।
एक वृत्त का क्षेत्रफल 616 वर्ग सेमी है। इस वृत्त के बाहर 2 मीटर चौड़ाई का मार्ग है। उस मार्ग का क्षेत्रफल कितना होगा।
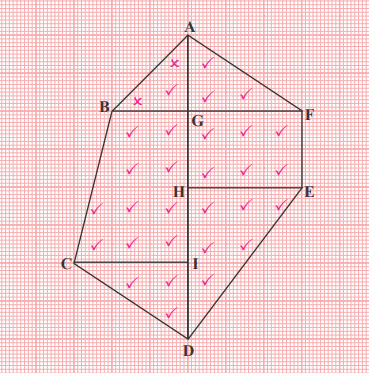
वर्ग ग्रिड द्वारा बहुभुज का अनुमानित क्षेत्रफल-
बहुभुज ABCDEFA में,
पूरे तथा आधे से बड़े वर्गों की संख्या=29
ठीक आधे वर्गों की संख्या=2
ठीक पूरे वर्गों की संख्या=29+1/2 x2
अतः बहुभुज ABCDEFA का क्षेत्रफल=29+1=30 वर्ग सेमी.
सूत्र द्वारा बहुभुज के क्षेत्रफल की गणना-
बहुभुज ABCDEFA का क्षेत्रफल = त्रिभुज AGB का क्षेत्रफल + समलम्ब चतुर्भुज BGIC का क्षेत्रफल + त्रिभुज CID का क्षेत्रफल + त्रिभुज DHE का क्षेत्रफल + आयत HEFG का क्षेत्रफल + त्रिभुज GFA का क्षेत्रफल
